Geometrie
Tělesa
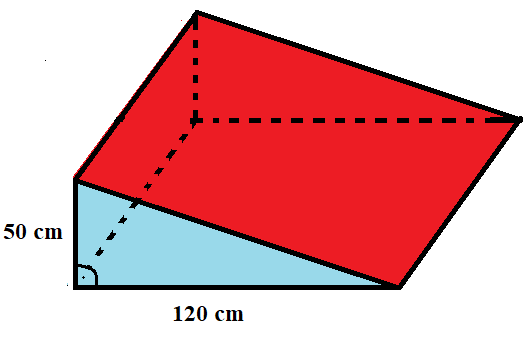
Ve skateparku stavěli novou překážku "skokánek". K výrobě potřebovali dvě desky trojúhelníkového tvaru jako bočnice, jednu čtvercovou desku na nájezd a jednu obdélníkovou desku na čelo překážky. Na spodní straně překážky nebylo žádné dřevo.
Chyba - zkus zadat jiný výsledek a klikni na opravit.