Přehled dovedností
Geometrie
V rovině leží pravoúhlý lichoběžník s pravým úhlem u vrcholu B. Základna AB má délku 12 cm a základna CD má délku 8 cm. Úhlopříčka AC má délku 13 cm.
Chyba - zkus zadat jiný výsledek a klikni na opravit.
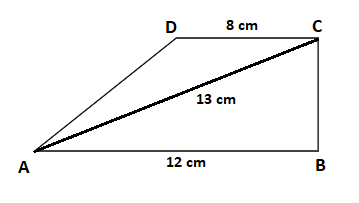
V rovině leží pravoúhlý lichoběžník s pravým úhlem u vrcholu B. Základna AB má délku 12 cm a základna CD má délku 8 cm. Úhlopříčka AC má délku 13 cm.
